Datapræsentation og 'den store tabel 1'
Ved formidling af forskningsresultater er det kutyme at give en præsentation af karakteristika for den undersøgte studiepopulation. Præsentationen samles ofte i artiklens første tabel, men på trods af, at denne type præsentation er allestedsnærværende i videnskabelige artikler, er der ofte nogen usikkerhed om, hvad den “store tabel 1” skal indeholde.
Det er værd at starte med at slå fast, at der ikke er nogle generelle, formelle krav til indholdet eller udformningen af den “store tabel 1”. I en videnskabelig artikel skal læseren overbevises om, at man kan begrunde artiklens konklusion gennem analyse af datamaterialet, så formålet og indholdet af den “store tabel 1” bør være at skitsere præmisserne (her studiepopulationen) så man lettere kan begrunde konklusionen.
Præsentationen af studiepopulationen tjener derfor to overlappende formål. For et første skal læseren kunne følge den videnskabelige argumentation, der leder hen til konklusionen, og for det andet kan læseren bruge oplysningerne om studiepopulationen til at vurdere, om studiepopulationen er sammenlignelig med andre populationer, som resultaterne fra artiklen dermed direkte kan overføres til.
Nedenfor er vist et fint eksempel på en illustrativ præsentation af en studiepopulation.1 Se The ORIGIN Trial Investigators (2012), “Basal Insulin and Cardiovascular and Other Outcomes in Dysglycemia”, New Eng J Medicine I artiklen sammenlignes to behandlinger - Insulin glargine og Standard care - i et randomiseret, kontrolleret studie, og hver af de relevante baggrundsvariable er opsummeret for de to randomiseringsgrupper. Tabellen præsenterer karakteristika ved de to delpopulationerne inden behandlingerne iværksættes.
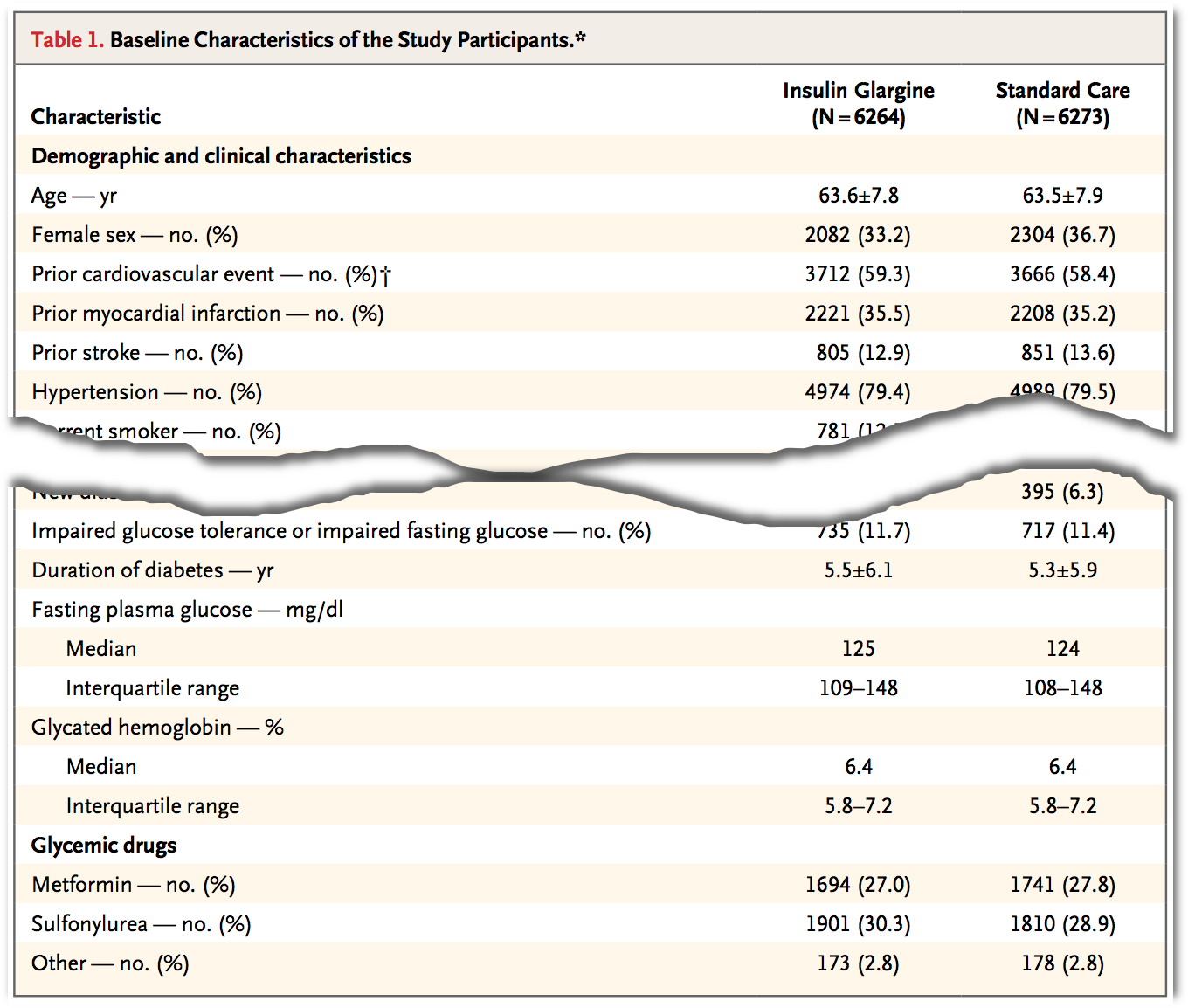
I tabellen præsenteres de enkelte variable på lidt forskellig vis efter deres type, og da der ikke er nogen fast præsentationsform er det en god ide at give en forklaring på, hvordan de enkelte tal i tabellen skal læses - enten direkte i tabellen eller som forklaring til den. I artiklen ovenfor står informationen både direkte i tabellen og i den tilhørende forklaring, hvor forfatterne specificerer, at “Plus-minus values are means \(\pm\) SD”. Læseren er derfor ikke i tvivl om, hvad de enkelte tal repræsenterer, hvad enten det er middelværdier, spredninger, medianer, andele osv.
Hvordan præsenterer man data?
Hvis formålet med “den store tabel 1” er at præsentere studiepopulationen, så gælder det om at formidle mest muligt information om hver variabel så kompakt som muligt. Forskellige datatyper opsummeres på forskellig vis, og i praksis afhænger det ikke kun at datatypen, men også af den enkelte variables fordeling.
Kategoriske variable opsummeres lettest ved at angive antallet af observationer (eventuelt med relative frekvenser) for hver kategori. Hvis der er mange kategorier med få observationer i hver, så kan det være nødvendigt at slå nogle af kategorierne sammen. Med denne tilgang får læseren hurtigt et overblik over de anvendte kategorier i datamaterialet, og samtidig får læseren en ide om fordelingen af observationer i de enkelte kategorier.
Tabel 1 nedenfor viser, hvordan man ofte præsenterer numeriske/kvantitative data. Kvantitative data plejer at blive opsummeret ved at angive en “typisk” måling, og ved at angive variationen i data. Ideen er, at den typiske måling skal angive centrum af fordelingen, mens variationen skal hjælpe læseren med at finde det område, hvor støresteparten af observationerne vil ligge.
Tabel 1: Ofte brugte mål til at beskrive typiske værdier og variationen for kvantitative variable (engelske udtryk i parentes).
| Typisk værdi | Variation |
|---|---|
| Typetal (mode) | Variationsbredde (range) |
| Middelværdi (mean) | Spredning (standard deviation) |
| Median | Inter-quartile range |
Typetallet og variationsbredden bliver ikke brugt så tit, fordi typetallet lider under, at værdien kan være ret ustabil, hvis den pågældende variabel kan antage mange forskellige værdier. Så vil langt de fleste værdier have frekvens 1, og dermed vil en enkelt dobbeltregistrering kunne ændre voldsomt på typetallet. Tilsvarende er variationsbredden plaget af, at man for det første ikke har nogen information omkring, hvordan den midterste del af fordelingen opfører sig, og desuden kan en enkelt ekstrem værdi have enorm indflydelse på hele variationsbredden.
Figur 1: To eksempler hvor typetallet og variationsbredden kommer i problemer. I det første eksempel har hver enkelt måling sin egen værdi, så der er ikke noget entydigt typetal, ligesom der heller ikke er noget klart typetal i eksempel 2. Begge eksempler har samme variationsbredde på trods af, at der er en klar forskel i fordelingen af observationerne i de to situationer.
Middelværdien og spredningen er nok de mest anvendte metoder til at opsummere fordelingen af en numerisk/kvantitativ variabel. Der er tre grunde til at middelværdien og spredningen er ekstra interessante at benytte til at beskrive en fordeling. For det første har stort set alle læsere en god fornemmelse for, hvad middelværdien er, og hvordan den skal fortolkes. Desuden består de fleste af de efterfølgende statistiske analyser af at undersøge forskelle i middelværdier, og derfor lægger brugen af middelværdien direkte op til at man kan se nogle af de værdier, som efterfølgende skal bruges. Ind imellem dukker forslag om at angive middelværdi \(\pm 2\cdot\) SE (standard error) i stedet for middelværdi \(\pm 2\cdot\) spredningen. Det er der egentlig ikke noget problem i, men det betyder, at fokus i tabellen bliver ændret, og at tabellen ikke længere præsenterer normal-/referenceområder for de undersøgte variable. Argumentet for at bruge SE skal i hvert fald ikke være, at grænserne bliver mindre - man skal bruge SE, hvis det er relevant at inkludere i forhold til den videnskabelige argumentation. Slutteligt er der den rare egenskab - hvis data følger en normalfordeling - at 95% af observationerne vil ligge indenfor middelværdien \(\pm 2\) gange spredningen. Med andre ord kan læseren let udregne et normalområde ud fra middelværdien og spredningen i de tilfælde, hvor data følger en normalfordeling.
Men måske bliver middelværdien og spredningen brugt lidt for ofte uden at der bliver tænkt over de situationer, hvor det ikke giver mening at sammenfatte en fordeling i middelværdien og spredningen. Middelværdien er følsom overfor outliers, og hvis fordelingen er skæv vil middelværdien bliver trukket i samme retning som skævheden. Desuden har middelværdien den lidt ubehagelig egenskab, at den kan give et resultat, der ikke svarer til nogle af de værdier man ser i datasættet: hvis fordelingen af data eksempelvis består af to lige store, adskilte pukler, så vil middelværdien ligge midt imellem disse pukler selvom der reelt set ikke optræder en eneste observationer i intervallet mellem de to pukler.
Hvis data ikke følger en normalfordeling er det i nogle tilfælde muligt at transformere data, så de transformerede data ligner en normalfordeling, og så giver det mening at udregne middelværdien og spredningen for de transformerede data. For de fleste læsere kan det dog være svært at forholde sig til transformerede værdier, men så kan man benytte middelværdi og spredning for de transformerede data til at udregne et normalområde, og så tilbagetransformere grænserne for normalområdet til den oprindelige skala. Et eksempel er vist i figuren nedenfor, der viser en højreskæv variabel.
Figur 2: For ikke-normalfordelte data vil middelværdien blive trukket i retning af halen, og spredningen vil ende med at passe dårligt på begge sider af middelværdien. Normalområder baseret på middelværdi \(\pm 2\) spredning vil derfor give en dårlig repræsentation af data. I dette tilfælde er den nedre grænse langt til venstre for, hvor vi har data, og den øvre grænse når ikke helt ud og dække målingerne i den højre ende af fordelingen. Grænserne for normalområdet bliver -0.57 og 17.34.
På figuren ses, at middelværdien (den sorte linje) bliver trukket i retning af halen, og grænserne for 95% normalområdet (de stiplede linjer) passer ikke særlig godt med data. Hvis vi derimod tager logaritmen til vores data har de nedenstående fordeling, der minder om en normalfordeling. Her giver det mening at udregne middelværdien og spredningen og bruge disse værdien til at konstruere et normalområde. Det bliver så et normalområde for de logaritmetransformerede data!
Figur 3: Efter logaritmetransformation er data pæne og 95% normalområdet går fra 1 til 3. Når vi tilbagetransformere disse værdier fås henholdsvis \(\exp(1)=2.71\) og \(\exp(3)=20.19\). Til sammenligning med resultaterne fra de originale data har vi fået rykket normalområdet længere mod højre, så det bedre dækker de reelle observationer.
I langt de fleste tilfælde giver det dog mening at bruge medianen til at repræsentere en enkelt “typisk” måling fra populationen. Medianen har den fordel, at den giver mening at benytte selv for skæve fordelinger, den kan bruges på ordinale data, den er robust overfor outliers, den angiver en dataværdi, som rent faktisk er observeret, og hvis data er normalfordelte vil den være tæt på sammenfaldende med middelværdien. Sammen med medianen bruges ofte inter-quartile range (IQR) til at angive variationen. IQR udregnes som forskellen mellem øvre og nedre kvartil (75% og 25% percentilerne) og angiver det spændet for de midterste 50% af observationerne. Ligesom medianen er IQR robust overfor outliers.
Det kan virke lidt urimeligt, at man med middelværdi \(\pm 2\) spredninger er interesseret i at beskrive de centrale 95% af observationerne, mens man med medianen og IQR “nøjes” med at beskrive de midterste 50%. Der er dog ikke noget til hinder for at bruge samme princip til at finde de midterste 95% af observationerne og angive disse grænser i den “store tabel 1”. Det er faktisk den løsning, jeg selv bedst kan lide. Vi skal bruge 2.5% og 97% percentilerne som grænser, hvis vi er interesseret i de midterste 95% af observationerne. Man kan tænke på det som om, at vi skærer 2.5% af observationerne fra i fordelingens venstre side og 2.5% fra i fordelingens højre side. Ulempen ved at gå til disse yderlige percentiler er, at robustheden forsvinder medmindre man har mange data, fordi man skal finde en grænse ude i halen af fordelingen, hvor der ikke er så megen information. Denne usikkerhed er dog også til stede ved de andre metoder, der anvendes til at afrapportere variationen (spredning og range): det er et generelt problem, når man har få data til rådighed. Der findes naturligvis også situationer, hvor medianen kommer til kort. Det er svært at gengive al informationen omkring en variabel i bare et enkelt tal eller to, hvis fordelingen eksempelvis har flere adskilte toppe, har form som et ‘U’, eller blot er meget varierende. I de tilfælde kan den bedste løsning være simpelthen at vise et histogram over data, så læseren selv kan danne sig et overblik over variablens kompleksitet.
Tommelfingerreglen for numeriske data er derfor, at benytte middelværdien og spredningen til at præsentere normalfordelte data, og at bruge medianen og 2.5%/97.5% percentilerne (alternativt inter-quartile range) til at præsentere ikke-normalfordelte data. Uanset hvad man vælger at tage med i “den store tabel 1”, så er det vigtigste at huske, at tabellen skal hjælpe læseren med at forstå de data, der er brugt i undersøgelsen, så læseren bedre kan forstå resultaterne og de præmisser, som undersøgelsen bygger på.